class: center, middle, inverse, title-slide # Extracting topics 📚 from ## 🎗cancer patients’ mutational profiles ### Zhi Yang ### 2019-07-30 --- ## About this talk * ### For those who've never heard of it ❓ what make a topic model (i.e. Latent Dirichlet Allocation) 📚 its general application * ### For those who know about it 🎗️ Its use in cancer research 📊 data, modeling, software 🏥 medical implications --- ## We usually extract topics from: ### books, customer reviews, tweets, ... ### scientific journals, medical records, ... ### .red[what if they can't be "read"?] -- <center> <img src="imgs/tcga.png" width=70%> --- ## Why studying somatic mutations?  --- ## What do we need computers for? .center[ ### Volume ### Velocity ### Variety ### Variability ] .footnote[[Understanding big data themes from scientific biomedical literature through topic modeling ](https://link.springer.com/article/10.1186/s40537-016-0057-0)] --- # Data sources ### 10,952 exomes ### 1,048 whole-genomes ### 40 distinct types of human cancer #### The Cancer Genome Atlas (TCGA),the International Cancer Genome Consortium (ICGC), data from peer-reviewed journals .footnote[[Signatures of Mutational Processes in Human Cancer](https://cancer.sanger.ac.uk/cosmic/signatures)] --- # What are in a topic model? .pull-left[ ### documents ### topics ### words ] .pull-right[ ] --- # What are in a topic model? .pull-left[ ### documents ### .grey[topics] .red[--> latent] ### words ] .pull-right[ ] --- # In a single document .center[<img src="imgs/str.png" width=50%, hspace="30"> <img src="imgs/topics.png", width=40%>] .pull-bottom[ * ### every document is unique * ### each topic has different fractions, `[0, 1]` ] --- # In a topic .center[<img src="imgs/str.png", width=50%, hspace="30"> <img src="imgs/words.png", width=40%>] * ### Topics are consistent across documents * ### choosing the number of topics could be a headache 😟 --- # The hierarchical structure .center[<img src="imgs/topics.png", width=40%> <img src="imgs/words.png", width=40%>] * ### a single .red[document] contains .red[topics] with .red[weights] * ### a .red[topic] is a unique distribution of .red[words] --- # LDA Topic Modeling on emojis <img src="https://github.com/lettier/lda-topic-modeling/raw/master/static/png/screenshot.png"> .footnote[https://lettier.com/projects/lda-topic-modeling/] --- # Data collection <br> .center[<img src="imgs/dataprocess.png" width=60%> ### .red[Tissue ➡Sequencing ➡ input]] -- .pull-left[ |sample|chr|position|ref|alt| |---|:---:|:---:|:--:|:--:| |sample1|chr1|100|A|C |sample1|chr2|100|G|T |sample2|chr1|300|T|C |sample3|chr3|400|T|C ] -- .pull-right[ ### .center[.red[? ?] A>C .red[? ?] ] ### .center[G T A>C T C] ] --- ## A glimpse of mutational profiles <br>  .footnote[[Yang et al. HiLDA: a statistical approach to investigate differences in mutational signatures, 2019](https://www.biorxiv.org/content/10.1101/577452v1)] --- # Where are those "words"? <img src="imgs/1536.png"> --- ## Topics made of words <img src="https://d2908q01vomqb2.cloudfront.net/f1f836cb4ea6efb2a0b1b99f41ad8b103eff4b59/2018/05/22/sagemaker-ntm-6.gif"> .footnote[[Introduction to the Amazon SageMaker Neural Topic Model ](https://aws.amazon.com/blogs/machine-learning/introduction-to-the-amazon-sagemaker-neural-topic-model/)] --- ## Topics made of mutations .center[<img src="imgs/sigs.png" width=60%>] .footnote[[Shiraishi et al. A simple model-based approach to inferring and visualizing cancer mutation signatures, PLoS Genetics, 2015](https://journals.plos.org/plosgenetics/article?id=10.1371/journal.pgen.1005657)] --- ## Topics made of mutations .center[<img src="imgs/Signature_patterns.png" width=65%>] .footnote[[Signatures of Mutational Processes in Human Cancer](https://cancer.sanger.ac.uk/cosmic/signatures)] --- .center[<img src="imgs/membership.PNG" width="80%">] .footnote[[Shiraishi et al. A simple model-based approach to inferring and visualizing cancer mutation signatures, PLoS Genetics, 2015](https://journals.plos.org/plosgenetics/article?id=10.1371/journal.pgen.1005657)] --- ## Association with known risk factors .center[.pull-top[ <img src="imgs/smoking.png" width=30%> <img src="imgs/sunlight.png" width=30%> <img src="imgs/pole.png" width=30%> ]] .center[ .pull-bottom[    ] ] .footnote[[Shiraishi et al. A simple model-based approach to inferring and visualizing cancer mutation signatures, PLoS Genetics, 2015](https://journals.plos.org/plosgenetics/article?id=10.1371/journal.pgen.1005657)] --- ## Software implementation * R package and Shiny app: **pmsignature** <img src="imgs/panel.png" width=25%> <img src="imgs/analysis.png" width=70%> .footnote[[Shiraishi et al. A simple model-based approach to inferring and visualizing cancer mutation signatures, PLoS Genetics, 2015](https://friend1ws.shinyapps.io/pmsignature_shiny/)] --- ## Hierarchical topic model .pull-left[ ### documents ### topics .red[--> weights] ### words ] .pull-right[  ] --- ## After applying the topic model,  .center[Are they different?] --- ## Statistical inference .center[<img src="imgs/twogroups.png" width =90%>] --- ## Group differences fractions `\(p_k\)` and concentration parameters `\(\alpha_k\)` `$$p_1, \cdots, p_K \sim Dirichlet(\alpha_1,\cdots,\alpha_K)$$` `$$\mu_k = \frac{\alpha_k}{\sum_k{\alpha_k}}$$` To capture the group difference for signature `\(i\)`, `$$\Delta_i = \mu^{(1)}_i - \mu^{(2)}_i$$` What we'd like to know, `$$H_0: \Delta_i = 0, i = 1, 2,..., K$$` <br> .red[Why don't we just compare the estimated values?] `$$\Delta_i = \hat{\mu}^{(1)}_i - \hat{\mu}^{(2)}_i$$` --- ## Potentiaized treatment 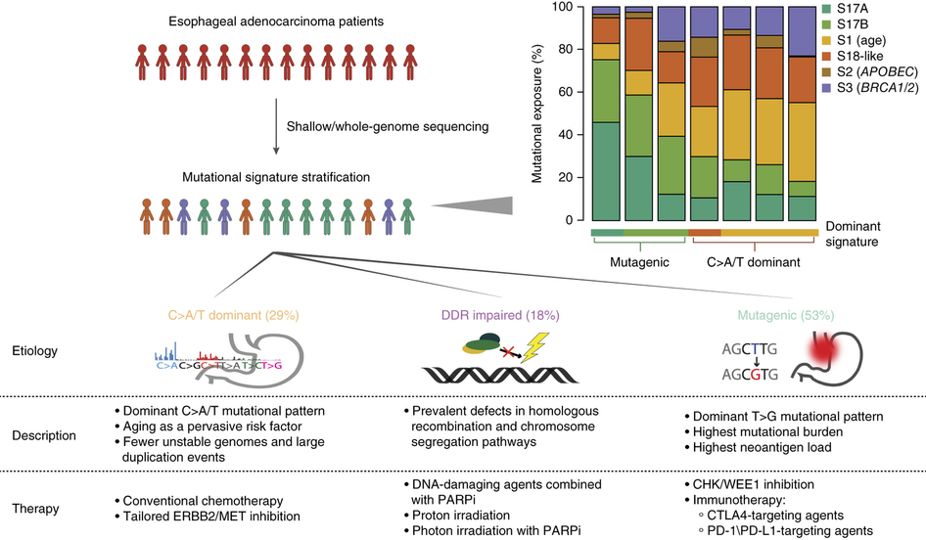 .footnote[[Proposed subclassification of EAC based on mutational signatures](https://www.nature.com/articles/ng.3659)] --- # A mini GO~~T~~B family tree 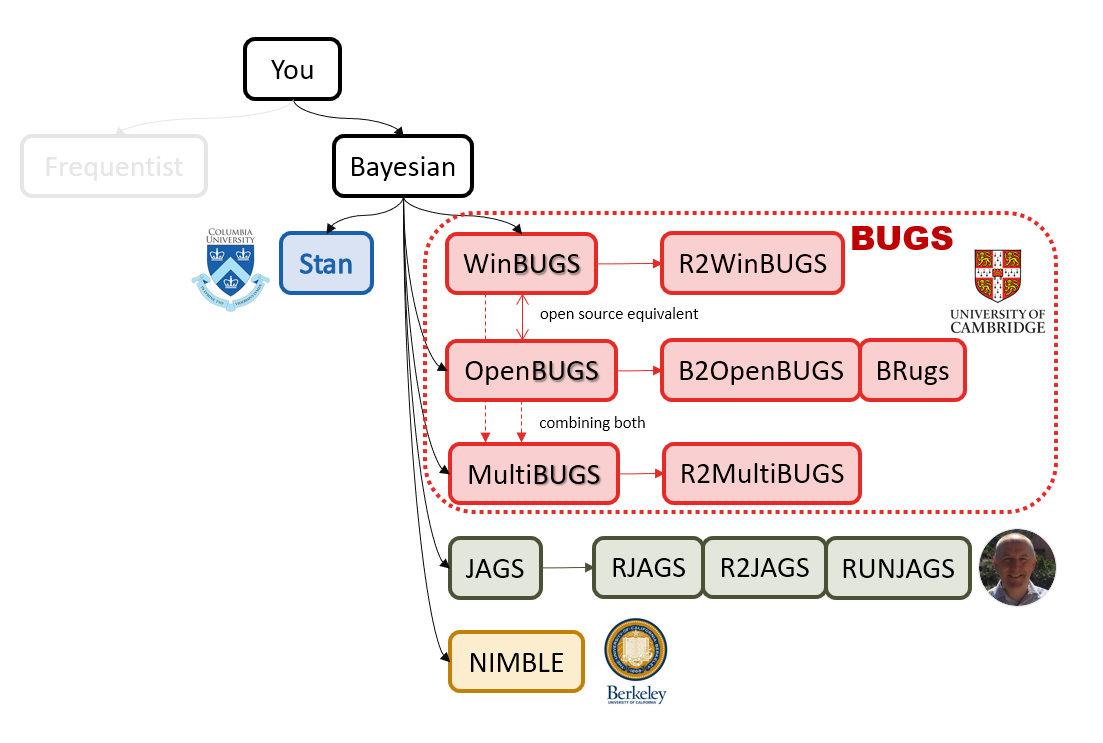 --- class: center, middle # .red[Why Bayesian?] -- ### You learn from the data -- ### You know the uncertainty of the estimated parameters .left[.footnote[[My Journey From Frequentist to Bayesian Statistics](http://www.fharrell.com/post/journey/)]] --- class: center, middle #.red[JAGS] ###stands for #.red[Just Another Gibbs Sampler] ### developed by Martyn Plummer <img src="imgs/mp.jpg" width="20%"> --- class: center, middle #.red[Why JAGS?] ###why not WinBUGS 🐞 or Stan? --- #JAGS vs. WinBUGS ### WinBUGS is historically very important with slow development -- ### JAGS has very similar syntax to WinBUGS and it allows cross-platform -- ### Great interface to **.blue[R]**! .small[(rjags, R2jags,runjags)] .footnote[ [When there is WinBUGS already, why is JAGS necessary?](https://www.quora.com/When-there-is-WinBUGS-already-why-is-JAGS-necessary) ] --- .pull-left[ # .red[JAGS] * longer history with tons of resources 📕📝🎓 * easy to learn and run it * need to recompile model * fewer developers * less viz tools * various MCMC sampling methods ] .pull-right[ # .blue[Stan] * A newer tool with great team/active community * steeper learning curve * no need to recompile * Syntax check in **.blue[R]** 😱 * ShinyStan (applicable to JAGS) * require fewer iterations to converge ] .center[### Which one's faster? Inconclusive] ### .red[My situation] Stan doesn't support discrete sampling .footnote[ [Stan vs. WinBugs: A search for informed opinions](https://www.reddit.com/r/statistics/comments/5on87q/stan_vs_winbugs_a_search_for_informed_opinions/) ] --- #.red[Why me?] ### I wrote a part of my dissertation with **JAGS** ### I've repeatedly read through **JAGS**, WinBUGS manual and numerous journals ### I've four years' experiences with searching **JAGS** examples in Google and GitHub --- # Installation ### Install **R** ### Install **RStudio** ### Install the **JAGS** from https://sourceforge.net/projects/mcmc-jags/ ### Install the **R2jags** package from [CRAN](https://cran.r-project.org/web/packages/R2jags/index.html): ```r install.packages("R2jags") library(R2jags) ``` --- class: center, middle # Shiny Demo The focus of the analysis presented here is on accurately estimating the mean of IQ using simulated data. [FBI: First Bayesian Inference](https://www.rensvandeschoot.com/fbi-the-app/) <img src="imgs/shiny.png" width="90%"> .footnote[https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4158865/] --- # Strong prior vs. weak prior 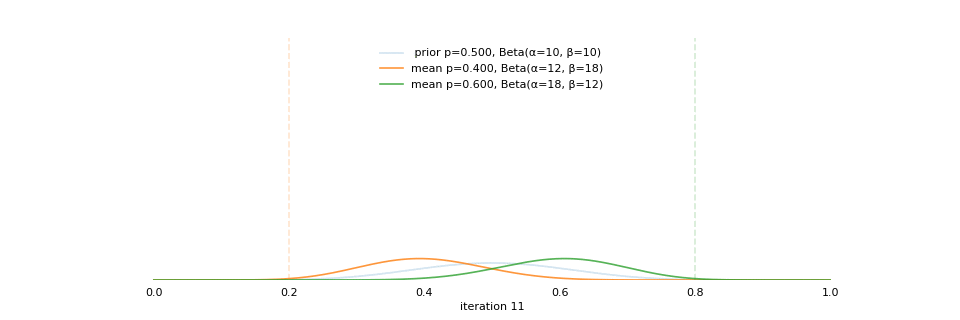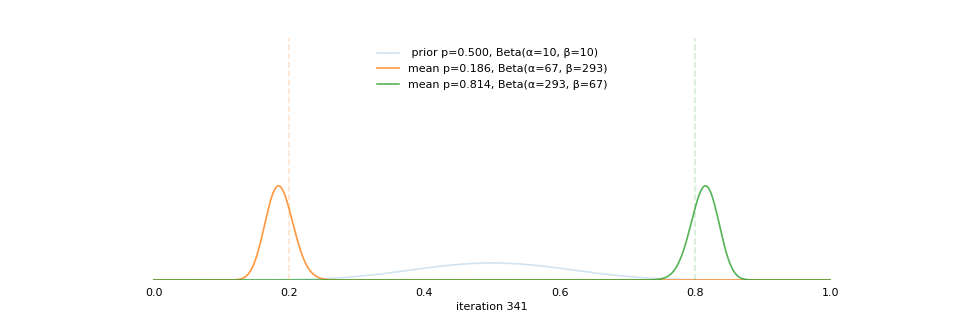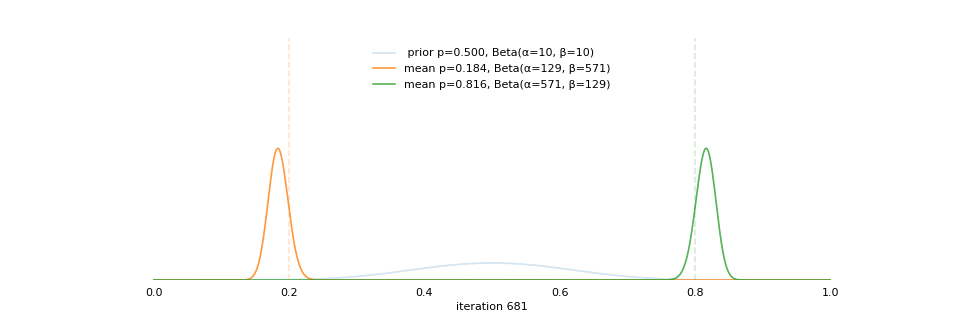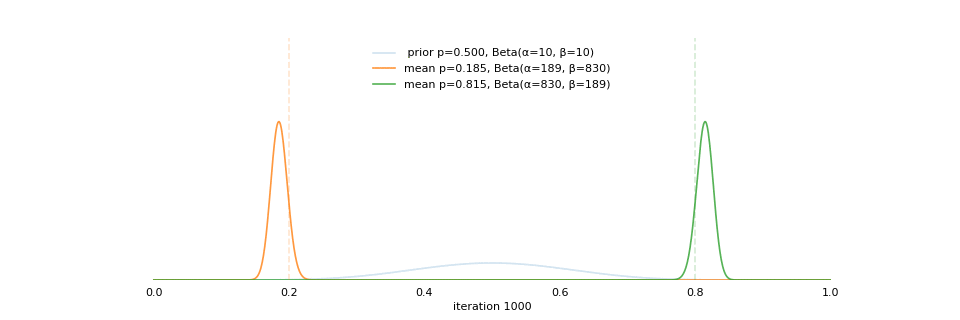  .footnote[https://towardsdatascience.com/visualizing-beta-distribution-7391c18031f1] --- # Let's get started! We hold meetings every month and post it on meetup.com, which tells us how many people've signed up, `\(n\)`. But not everyone show up (i.e., traffic). So, we'd like to know what percentage of people, `\(\theta\)`, will show up to order enough pizzas. .center[ `\(Y_i|\theta \sim Binom(n_i, \theta)\)` `\(\theta \sim Beta(a, b)\)` ] Weak prior: .center[ `\(Beta(1, 1) \leftrightarrow Unif(0, 1)\)` ] ```r Y <- c(77, 62, 30) N <- c(39, 29, 16) ``` --- # Write the model But as you know, someone (@lukanegoita) said <center><img src="imgs/meme.png" width="60%"> --- # Write the model .center[ `\(Y_i|\theta \sim Binom(n_i, \theta)\)` `\(\theta \sim Beta(a, b)\)` ] .pull-left[ In .blue[R] ```r model{ for(i in 1:3){ Y[i] <- rbinom(1, N[i], theta) } theta <- rbeta(1, 1, 1) } ``` ] .pull-right[ In .red[JAGS] ```r model{ for(i in 1:3){ Y[i] ~ dbinom(theta, N[i]) } theta ~ dbeta(1, 1) } ``` ] - A variable should appear **only once** on the left hand side - A variable may appear multiple times on the right hand side - variables that only appear on the right must be supplied as **data** --- # Tips on syntax #### No need for variable declaration #### No need for semi-colons at end of statements #### use d`dist` instead of r`dist` for random sampling #### dnorm(mean, **precision**) .red[not] dnorm(mean, **sd**) #### It allows matrix and array #### It is .red[illegal] to offer definitions of the variable twice --- # Write the model ```r library(R2jags) model_string<-"model{ # Likelihood for(i in 1:3){ Y[i] ~ dbinom(theta, N[i]) } # Prior theta ~ dbeta(1, 1) } " # Data N <- c(77, 62, 30) Y <- c(39, 29, 16) # specify parameters to be monitered params <- c("theta") ``` --- # rjags vs. runjags vs. R2jags #### `R2jags` and `runjags` are just wrappers of rjags #### `runjags` makes it easy to run chains in parallel on multiple processes #### `R2jags` allows running until converged and paralleling MCMC chains #### Otherwise, they all have very similar syntax and pre-processing steps --- # Choosing `R2jags` ```r output <- jags(model.file = textConnection(model_string), data = list(Y = Y, N = N), parameters.to.save = params, n.chains = 2, n.iter = 2000) ``` ``` ## Compiling model graph ## Resolving undeclared variables ## Allocating nodes ## Graph information: ## Observed stochastic nodes: 3 ## Unobserved stochastic nodes: 1 ## Total graph size: 8 ## ## Initializing model ## ## | | | 0% | |++ | 4% | |++++ | 8% | |++++++ | 12% | |++++++++ | 16% | |++++++++++ | 20% | |++++++++++++ | 24% | |++++++++++++++ | 28% | |++++++++++++++++ | 32% | |++++++++++++++++++ | 36% | |++++++++++++++++++++ | 40% | |++++++++++++++++++++++ | 44% | |++++++++++++++++++++++++ | 48% | |++++++++++++++++++++++++++ | 52% | |++++++++++++++++++++++++++++ | 56% | |++++++++++++++++++++++++++++++ | 60% | |++++++++++++++++++++++++++++++++ | 64% | |++++++++++++++++++++++++++++++++++ | 68% | |++++++++++++++++++++++++++++++++++++ | 72% | |++++++++++++++++++++++++++++++++++++++ | 76% | |++++++++++++++++++++++++++++++++++++++++ | 80% | |++++++++++++++++++++++++++++++++++++++++++ | 84% | |++++++++++++++++++++++++++++++++++++++++++++ | 88% | |++++++++++++++++++++++++++++++++++++++++++++++ | 92% | |++++++++++++++++++++++++++++++++++++++++++++++++ | 96% | |++++++++++++++++++++++++++++++++++++++++++++++++++| 100% ## | | | 0% | |** | 4% | |**** | 8% | |****** | 12% | |******** | 16% | |********** | 20% | |************ | 24% | |************** | 28% | |**************** | 32% | |****************** | 36% | |******************** | 40% | |********************** | 44% | |************************ | 48% | |************************** | 52% | |**************************** | 56% | |****************************** | 60% | |******************************** | 64% | |********************************** | 68% | |************************************ | 72% | |************************************** | 76% | |**************************************** | 80% | |****************************************** | 84% | |******************************************** | 88% | |********************************************** | 92% | |************************************************ | 96% | |**************************************************| 100% ``` ``` ## Compiling model graph ## Resolving undeclared variables ## Allocating nodes ## Graph information: ## Observed stochastic nodes: 3 ## Unobserved stochastic nodes: 1 ## Total graph size: 9 ## ## Initializing model ## ## | | | 0% | |++ | 4% | |++++ | 8% | |++++++ | 12% | |++++++++ | 16% | |++++++++++ | 20% | |++++++++++++ | 24% | |++++++++++++++ | 28% | |++++++++++++++++ | 32% | |++++++++++++++++++ | 36% | |++++++++++++++++++++ | 40% | |++++++++++++++++++++++ | 44% | |++++++++++++++++++++++++ | 48% | |++++++++++++++++++++++++++ | 52% | |++++++++++++++++++++++++++++ | 56% | |++++++++++++++++++++++++++++++ | 60% | |++++++++++++++++++++++++++++++++ | 64% | |++++++++++++++++++++++++++++++++++ | 68% | |++++++++++++++++++++++++++++++++++++ | 72% | |++++++++++++++++++++++++++++++++++++++ | 76% | |++++++++++++++++++++++++++++++++++++++++ | 80% | |++++++++++++++++++++++++++++++++++++++++++ | 84% | |++++++++++++++++++++++++++++++++++++++++++++ | 88% | |++++++++++++++++++++++++++++++++++++++++++++++ | 92% | |++++++++++++++++++++++++++++++++++++++++++++++++ | 96% | |++++++++++++++++++++++++++++++++++++++++++++++++++| 100% ## | | | 0% | |** | 4% | |**** | 8% | |****** | 12% | |******** | 16% | |********** | 20% | |************ | 24% | |************** | 28% | |**************** | 32% | |****************** | 36% | |******************** | 40% | |********************** | 44% | |************************ | 48% | |************************** | 52% | |**************************** | 56% | |****************************** | 60% | |******************************** | 64% | |********************************** | 68% | |************************************ | 72% | |************************************** | 76% | |**************************************** | 80% | |****************************************** | 84% | |******************************************** | 88% | |********************************************** | 92% | |************************************************ | 96% | |**************************************************| 100% ``` --- # Visualizing output ```r plot(as.mcmc(output)) ``` <!-- --> --- # Visualizing output ```r library(mcmcplots) mcmcplot(as.mcmc(output),c("theta")) denplot(as.mcmc(output),c("theta")) ```  --- # Model diagnostic So it might take a longer time for run <center><img src="imgs/meme2.png" width="60%"> --- ## Model diagnostic and convergence ```r output$BUGSoutput$summary ``` ``` ## mean sd 2.5% 25% 50% 75% ## deviance 14.6755846 1.3992791 13.6488245 13.7614902 14.1370965 15.0345916 ## theta 0.4973384 0.0388237 0.4187856 0.4710636 0.4970235 0.5249785 ## 97.5% Rhat n.eff ## deviance 18.7558006 1.017801 220 ## theta 0.5720824 1.003696 2000 ``` If it fails to converge, we can do the following, ```r update(output, n.iter = 1000) autojags(output, n.iter = 1000, Rhat = 1.05, n.update = 2) ``` --- # weak prior vs. strong prior ```r output$BUGSoutput$summary ``` ``` ## mean sd 2.5% 25% 50% 75% ## deviance 14.6755846 1.3992791 13.6488245 13.7614902 14.1370965 15.0345916 ## theta 0.4973384 0.0388237 0.4187856 0.4710636 0.4970235 0.5249785 ## 97.5% Rhat n.eff ## deviance 18.7558006 1.017801 220 ## theta 0.5720824 1.003696 2000 ``` ```r output2$BUGSoutput$summary ``` ``` ## mean sd 2.5% 25% 50% 75% ## deviance 15.2841452 1.77163845 13.6509996 13.9603596 14.6893500 16.0268236 ## theta 0.5357841 0.02994589 0.4754806 0.5161242 0.5361084 0.5560317 ## 97.5% Rhat n.eff ## deviance 20.0407688 1.005639 490 ## theta 0.5934454 1.002685 690 ``` --- # weak prior vs. strong prior .pull-left[ ```r denplot(as.mcmc(output), parms = "theta", xlim = c(0.3, 0.7)) ``` <!-- --> ] .pull-right[ ```r denplot(as.mcmc(output2), parms = "theta", xlim = c(0.3, 0.7)) ``` <!-- --> ] --- #Linear regression .pull-left[ In .red[JAGS] ```r model<-"model{ # Likelihood for(i in 1:N){ y[i] ~ dnorm(mu[i], tau) mu[i] <- beta0 + beta1*x[i] } # Prior # intercept beta0 ~ dnorm(0, 0.0001) # slope beta1 ~ dnorm(0, 0.0001) # error term tau ~ dgamma(0.01, 0.01) sigma <- 1/sqrt(tau) }" lm_output <- jags(model.file = textConnection(model), data = list(y = y, x = x, N=15), parameters.to.save = c("beta0","beta1", "sigma"), n.chains = 2, n.iter = 2000, progress.bar ="none") ``` <br> ] .pull-right[ In .blue[R] ```r lm(y~x) ``` In statistics 101 `\(Y_i = b_0 + b_1X_i + \sigma\)` `\(Y \sim N(b_0 + b_1X, \sigma^2)\)` ] ``` ## Compiling model graph ## Resolving undeclared variables ## Allocating nodes ## Graph information: ## Observed stochastic nodes: 15 ## Unobserved stochastic nodes: 3 ## Total graph size: 70 ## ## Initializing model ``` --- # Interpretation .pull-left[ In .red[JAGS] ```r lm_output$BUGSoutput$summary[1:2, c(3,7)] ``` ``` ## 2.5% 97.5% ## beta0 -8.853992 52.131691 ## beta1 -16.496277 3.192873 ``` 95% credible interval ] .pull-right[ In .blue[R] ```r confint(lm(y~x)) ``` ``` ## 2.5 % 97.5 % ## (Intercept) -9.32782 51.322335 ## x -16.19329 3.486528 ``` 95% confidence interval ] --- #An alternative way .pull-left[ In .red[runjags] ```r model <- template.jags( y ~ x, data, n.chains=2, family='gaussian') ``` ] .pull-right[ In .blue[R] ```r lm(y~x) ``` ] --- # About sources 📕+💻 .pull-left[ #### If you've got 2hrs: - useR! International R User 2017 Conference JAGS [workshop](https://channel9.msdn.com/Events/useR-international-R-User-conferences/useR-International-R-User-2017-Conference/Introduction-to-Bayesian-inference-with-JAGS) by Martyn Plummer <-- 👨 of **JAGS** ] .pull-right[ #### If you've got 5 mins: [RJAGS: how to get started](https://www.rensvandeschoot.com/tutorials/rjags-how-to-get-started) by Rens van de Schoot, retweeted by Martyn Plummer ] #### <center> If you're a book lover: <center><img src="imgs/book2.png" width=25%> <img src="imgs/book.jpg" width=26%> --- # What about puppies? "perky ears" + "floppy ears" ?= "half-up ears" <img src="imgs/dogs.png"> --- # More ... - [CRAN Task View: Bayesian Inference](https://cran.r-project.org/web/views/Bayesian.html) - ["Selling" Stan](https://discourse.mc-stan.org/t/selling-stan/3693/9) - Seo-young Silvia Kim's Stan [talk](https://github.com/laRusers/presentations/blob/master/2019-07-08_stan/larusers-kim.pdf) <img src="imgs/stan.png" width=60%> --- class: center, middle # Thanks! and Keep in touch Slides: https://lda-mutations.netlify.com/ <i class="fab fa-twitter "></i> [@zhiiiyang](https://twitter.com/zhiiiyang) <i class="fab fa-github "></i> [zhiiiyang](https://github.com/zhiiiyang) <i class="fas fa-envelope "></i> [zyang895@gmail.com](mailto:zyang895@gmail.com) Slides created via the R package [**xaringan**](https://github.com/yihui/xaringan) and [**xaringanthemer**](https://github.com/gadenbuie/xaringanthemer)